Подстраховка Вейбуллом
Моя старая статья “К вопросу о распределении Lead Time” остается популярной и сегодня. Я написал ее более пяти лет назад, основываясь на практике и исследованиях 5-7-летней давности. Люди продолжают знакомиться со статьей, ссылаются на нее и задают мне вопросы о трактовке графиков распределения lead time. Иногда читатели спрашивают меня именно о распределении Вейбулла.
Хотя статья и выдержала серьезное испытание временем, не будут лишними некоторые уточнения.
Необходимо отметить особую роль распределения Вейбулла в попытках понять природу lead time (времени-в-процессе) профессиональных сервисов и умственного труда. Большое количество выборок lead time из реальной практики достаточно хорошо соответствует распределению Вейбулла. И, конечно, существуют выборки, которые не соответствуют такому распределению. Упрощающее допущение о том, что данные о lead time по каждому новому сервису предположительно будут соответствовать распределению Вейбулла, приводило нас к определенным открытиям и выводам. Впоследствии оказалось, что мы можем отказаться от “допущения Вейбулла”, но инсайты и практические советы по его результатам останутся в силе.
Таким образом, распределение Вейбулла служило для нас интеллектуальной подстраховкой или «четырехколесным велосипедом». По мере того , как Канбан-метод становился более зрелым за счет многолетнего международного опыта применения, его методологические принципы, связанные с lead time, подтвердились и стали аксиомой. «Четырехколесный велосипед» стал не нужен.
Распределение Вейбулла помогло мне понять практическое значение статистических функций отказа в умственной работе. Отказ подразумевает отношение двух вероятностей: вероятности того, что нерешенная ранее проблема будет решена в следующий момент времени, и вероятности того, что проблема останется нерешенной с начала такого момента времени до текущего.
Напомню, что мы занимаемся коллаборативным решением проблем и поставкой решений пользователям, которые хотят знать сколько времени это займет.
Приведу несколько возможных сценариев:
- Если наша функция отказа является константой, то распределение lead time будет экспоненциальным
- Если наша функция отказа — убывающая (что может произойти в случае плохой приоритизации, неявных классов обслуживания, плохо управляемых непредвиденных зависимостей от других сервисов — другими словами, из-за проблем, которые с высокой вероятностью могут возникнуть в профессиональных сервисах), то распределение lead time будет суб-экспоненциальным. Такая ситуация также известна как Крайнестан. Нассим Талеб называет ее Эффектом Линди. Проблема, которая оставалась нерешенной длительное время, вероятно, останется без решения и дальше. Сервисы с таким lead time практически непредсказуемы и не соответствуют потребностям клиентов. Практический совет при такой ситуации: сокращать и митигировать риск путем “отрезания хвоста” и повышения соответствия сервиса потребностям клиентов.
- Если наша функция отказа возрастает быстрее линейной функции, распределение lead time будет с низкой дисперсией. Все риски в нашем сервисе обладают коротким хвостом распределения. Это сигнал того, что мы дезорганизованы. Можете ли Вы предположить, что может в такой ситуации сделать Ваш бизнес?
- Если наша функция отказа возрастает, но медленнее, чем линейная функция (что может случиться благодаря включению обратной связи от клиентов в наши активности по решению проблем и благодаря хорошему управлению задержками и зависимостями, сохраняющему их вне Крайнестана), мы попадаем в так называемый Домен Хорошо управляемой Умственной Работы. Гики могут называть его Пограничный Среднестан.
Из всех распределений в семействе Вейбулла те, у которых значение параметра формы соответствует 1<k<2, находятся в счастливом среднем домене хорошо управляемой умственной работы. Распределение с k=1,5 представляет пример распределения из такого домена. Распределения Вейбулла с k<1 находятся в Крайнестане и домене непредсказуемых сервисов “бросай-все-и-чини”. Распределения Вейбулла с k>2 относятся к Центральному Среднестану, в домене “Вы не делаете умственной работы, на грани развала”. Распределения с k=1 и k=2 обозначают границы.
Интересный факт, что теперь мы можем отказаться от “Допущения Вейбулла” (в реальности распределения lead time могут быть, а могут и не быть распределениями Вейбулла) и три домена никуда не исчезнут. Любое распределение соответствует одному домену из такой тройки. Теперь мы можем задаться вопросом, какому домену соответствует ваш процесс? Далее мы можем предложить вам практически ценное руководство к действию — три разных пути.
Допущение (но не всегда корректное, насколько вы успели узнать) о том, что распределение lead time является распределением Вейбулла, позволяло нам думать в простых категориях формы и масштаба. Форма (в случае с распределением Вейбулла это равнозначно параметру формы) выражала всю информацию о паттернах рисков и задержек в сервисе. Параметр масштаба говорит нам о том, какие единицы времени отложены по горизонтальной оси.
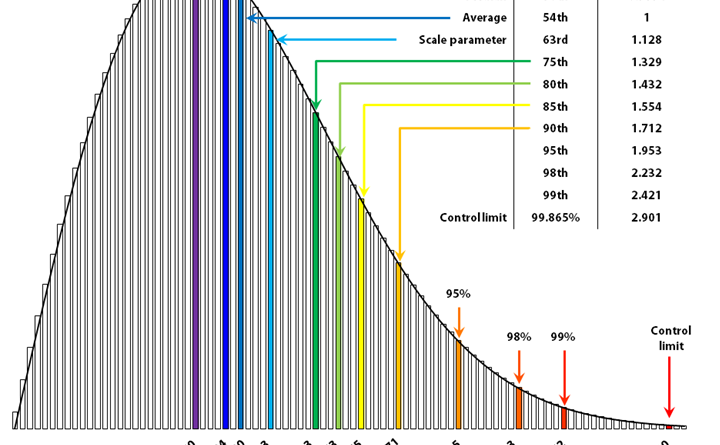
Теперь уберем допущение Вейбулла. Паттерны рисков и источников задержек продолжают определять форму, только теперь не в численном виде, а в виде линии графика распределения lead time, который менеджер приносит на встречу по обзору сервиса. И Вам все еще важно знать временную шкалу по оси Х: насколько быстро вы поставляете результат при типичном, умеренно-оптимистичном сценарии? Измеряется ли это время в часах? в днях? неделях? месяцах? Если первичным источником для ответа на это вопрос являются ваши “эмпирические” данные, то правильной привычкой будет наблюдение за 60-ым и 70-ым процентилями. Математики могут определить верхнюю границу доверительного интервала для оценки медианы значений lead time. При типичном размере выборок lead time, собираемых и используемых менеджерами в профессиональных сервисах, верхняя (правая) граница ожидаемо находится правее (“восточнее”) 60-ого процентиля. Что полностью совпадает с точкой формоинвариантного 63-его процентиля кривой распределения Вейбулла. И это справедливо для любого распределения, как Вейбулла, так и другого.
Как вы можете видеть, распределение Вейбулла служило нам в качестве «четырехколесного велосипеда» несколько лет назад, но сегодня необходимость в нем отпала. Практические рекомендации Канбан-метода по управлению lead time профессиональных сервисов остаются актуальными. Мы также можем понимать источники задержек и довольно реалистично их моделировать. Мы можем применять такие модели для того, чтобы увидеть эффекты от мероприятий по улучшению сервиса. Далее мы можем приоритизировать мероприятия, способные дать наиболее сильный положительный эффект для наших клиентов.
Оригинальная статья опубликована Алексеем Жегловым 22 октября 2019
Перевод: Дмитрий Орлов
Редактура: Артур Нек

Спасибо за переводы!
«Показатель риска», «функция иска» и т. п. здесь и в других постах — неточно.
В оригинале hazard rate = функция отказов. Это конкретный термин, которым пользуются математики, статистики и инженеры, занимающиеся проблемами надежности оборудования (одним из которых был капитан Вейбулл).
Большое спасибо за комментарий, Алексей! Внес корректировки в текст.
В соседней статье тоже поправил. Спасибо!
Верхняяя (правая) граница доверительного интервала для оценки медианы (50-ого перцентиля) обычно находится правее («восточнее») 60-ого перцентиля, т. к. менеджеры проектов (сервисов, продуктовых линий) обычно обладают слишком маленькими выборками эмпирических данных для более точной оценки. Например, 90-процентный доверительный интервал для оценки 50-ого перцентиля по выборке из 30 наблюдений простирается от 35-ого до 65-ого.
Из всех распределений в семействе Вейбулла те, у которых значение параметра формы соответствует 1<k<2, находятся в счастливом среднем домене хорошо управляемой умственной работы. Распределение с k=1,5 представляет пример распределения из такого домена. Распределения Вейбулла с k2 относятся к Центральному Среднестану, в домене “Вы не делаете умственной работы, на грани развала”. Распределения с k=1 и k=2 обозначают границы.
Спасибо огромное! Сложная и интересная штука. Правильно ли я понимаю, что это перекликается с интенсивностью наработки на отказ?