Как сверить выборку с распределением Вейбулла в Excel
ОБНОВЛЕНИЕ: Данный пост все еще актуален, но есть новый: Как сверить выборку с распределением Вейбулла без Excel.
Предупреждение: это очень технический и практический пост.
Оказывается, распределение Вейбулла — довольно распространено среди статистических распределений времени производства в проектах по разработке ПО. Этот инсайт принадлежит Трою Магеннису (Troy Magennis), лидирующему эксперту по симуляциям проектов методом Монте-Карло . Он изучил данные с большого количества реальных проектов. Трой также объясняет как работа со знаниями и ее тенденция к увеличению объема и прерывистости ведет к такому распределению. Рекомендую подробнее изучить его работы на эту тему — за них он стал лауреатом Brickell Key Award. Инсайт о распределении Вейбулла независимо от Троя подтвердил другой лауреат Brickell Key Award, Ричард Хенсли (Richard Hensley). Он изучил большое количество данных из ИТ-подразделения крупной компании.
Совпадают ли ваши лид-таймы с распределением Вейбулла?
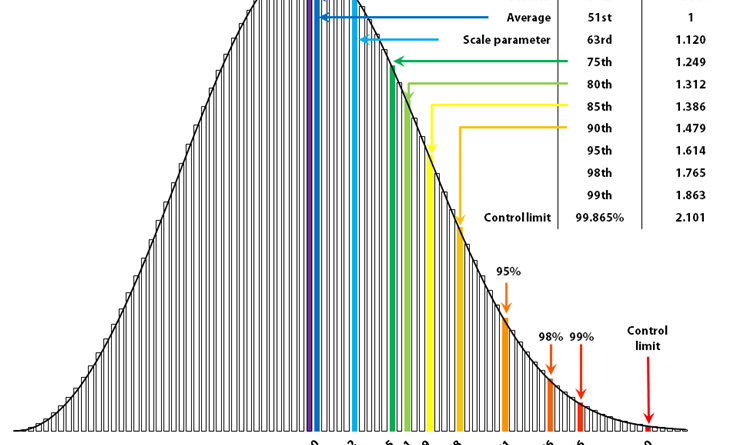
Вчера мне пришлось быстро ответить на этот вопрос, а под рукой оказались только Excel и мои знания о статистике. Распределение Вейбулла на самом деле — это группа распределений, формируемых параметром формы (k). На диаграмме выше видно, как изменение этого параметра влияет на форму кривой распределения. Распределение Вейбулла идентично экспоненциальному распределению при k=1 и распределению Рэлея при k=2. При иных значениях k происходит интерполяция/экстраполяция этих распределений. Итак, перед нами два вопроса:
- Соответствует ли данный набор значений распределению Вейбулла?
- Если соответствует, то чему равен параметр формы?
Вот простой алгоритм, которым вы можете следовать, чтобы ответить на эти вопросы для вашей выборки. Я приложу электронную таблицу в конце поста.
Шаг 1. Скопируйте ваш набор значений в колонку А электронной таблицы. Я предпочитаю оставлять первый ряд для заголовков столбцов, так чтобы значения начинались с ячейки А2.
Шаг 2. Отсортируйте значения в колонке А в порядке возрастания.
Шаг 3. Разделите интервал [0; 1] на равные интервалы, согласно количеству значений в вашей выборке. Внесите средние значения этих интервалов в колонку В. Если у вас N=100 значений, то формула Excel для этого будет =(2*ROW(B2)-3)/200 (200 == 2*N). Введите эту формулу в ячейку В2 и растяните на все ячейки колонки В.
Шаг 4. Заполните колонку С натуральными логарифмами значений колонки А. Введите формулу =LN(A2) в ячейку С2 и растяните ее на всю колонку.
Шаг 5. Заполните колонку D значениями, полученными из колонки В как описано дальше. Введите формулу =LN(-LN(1-B2)) в ячейку D2 и растяните ее до конца колонки. По сути, мы линеаризуем функцию накопительного распределения, чтобы линейная регрессия показала нам параметр формы.
Шаг 6. Если выборка совпадает с распределением Вейбулла, то параметр формы будет равен наклону прямой, проведенной через точки с координатами из колонок C и D. Для расчета используйте формулу =SLOPE(D2:D101,C2:C101) (Эта формула рассчитана на выборку, в которой N=100 значений — корректируйте ее исходя из своего количества значений). В приложенной электронной таблице это значение находится в ячейке G2.
Шаг 7. Посчитайте формулу =INTERCEPT(D2:101,C2:C101). (Ячейка G3)
Шаг 8. Посчитайте параметр масштаба для предыдущего шага =EXP(-G3/G2). (Ячейка G4)
Шаг 9. Проверьте, насколько хорошо совпадают значения при помощи формулы =RSQ(C2:C101,D2:D101). Если совпадение идеальное — значение будет равно 1.
Шаг 10. Если совпадение достаточно хорошее, можно еще раз проверить расчет на соответствие реальности. Для этого посчитайте среднее от полученных параметров формы и масштаба и сравните его с общим средним. Формула среднего

В Excel нет встроенной Гамма-функции, но есть функция, возвращающая ее логарифм. Таким образом, мы можем рассчитать прогнозируемое среднее по формуле =G4*EXP(GAMMALN(1+1/G2)). Теперь можно сравнить прогнозируемое среднее и общее среднее, которое получим формулой =AVERAGE(A2:A101).
Обновление
Есть и другой способ сделать линейную регрессию. Шаги выше сократят вертикальные расстояния (по направлению шкалы y) между лучшим совпадением кривой и точками выборки. Это возможно сделать и через сокращение горизонтальных расстояний. Второй метод последовательно переоценивает параметр формы, что нежелательно для практических применений аналитики лид-таймов. Это может приводить к неточностям, когда одно и то же значение встречается в выборке несколько раз, особенно на левой стороне распределения. По этим причинам, я рекомендую использовать метод, изначально описанный в оригинальном посте (линейная регрессия, сокращение вертикальных расстояний).
Я также обновил электронную таблицу более “умными” формулами. Теперь их не нужно корректировать — вне зависимости от количества значений в выборке лид-таймов.
Оригинальная статья опубликована Алексеем Жегловым 1 августа 2013
Перевод: Фролов Максим
Редактура: Артур Нек