Как сверить выборку с распределением Вейбулла без Excel

Чуть больше года назад я написал короткую, но довольно техническую статью. Там я ответил как сделать сверку выборки с распределением Вейбула без сложных статистических инструментов, опираясь только на то, что присутствует в  в большинстве современных офисов: ПО для электронных таблиц — Excel.

Вот проблема, которую мы стремимся решить. Распределение Вейбулла можно часто заметить в выборках лид-таймов поставки у различных творческих сфер деятельности. Нам нужно сопоставить выборку лид-таймов с распределением и узнать его параметры (форма и масштаб). Это поможет понять риски, установить ожидаемый уровень сервиса и создать модели прогнозирования.

Моя статья и электронная таблица с формулами все еще актуальны — просто вставьте туда свои данные. Тем не менее, хочу предложить еще более простой метод, который будет доступен большому кругу читателей. Он менее точный, но достаточно достоверный — вы можете использовать его “на ходу”, даже если под рукой нет более сложных инструментов.

3 основных формы и 2 пограничных кейса

Три основные формы кривых распределения Вейбулла можно отличить при рассмотрении выпуклости и вогнутости левой стороны и средней части кривой. (С правой стороны они всегда выпуклые) Три кейса соответствуют значению параметра формы (k):

1. меньше 1
2. между 1 и 2
3. больше 2

Экспоненциальное распределение (k=1) и распределение Рэлея(k=2) представляют собой пограничные кейсы, разделяющие 3 основных формы.

Посмотрим на графики.

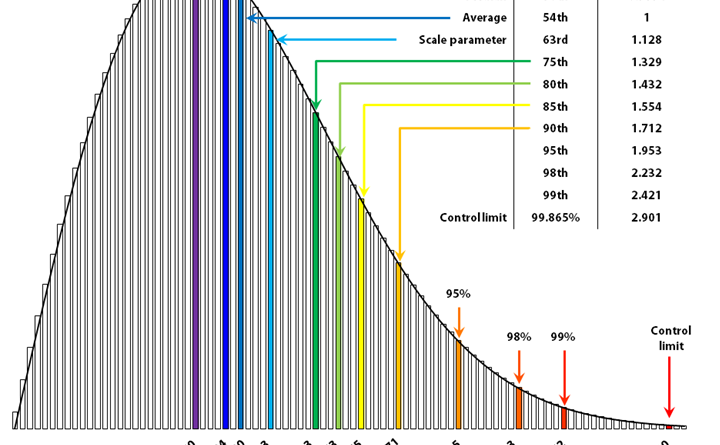
Когда параметр формы меньше 1, кривая распределения (функция плотности вероятностей) выпуклая на всём протяжении. Этот параметр формы часто наблюдают в IT, клиентском обслуживании, и других сферах с большим количеством незапланированной работы. Самое низкое значение, которое мне приходилось наблюдать: k=0.56. Я выбрал k=0.75, чтобы представить эту форму распределения. Основные визуальные черты, помимо выпуклости, это:

• сдвинутое вправо среднее значение (при k=0.75, оно попадает на 68 перцентиль)
• широкое распространение общих причин вариации (при k=0.75, отношение 99 перцентиля к медиане составляет 15:1)

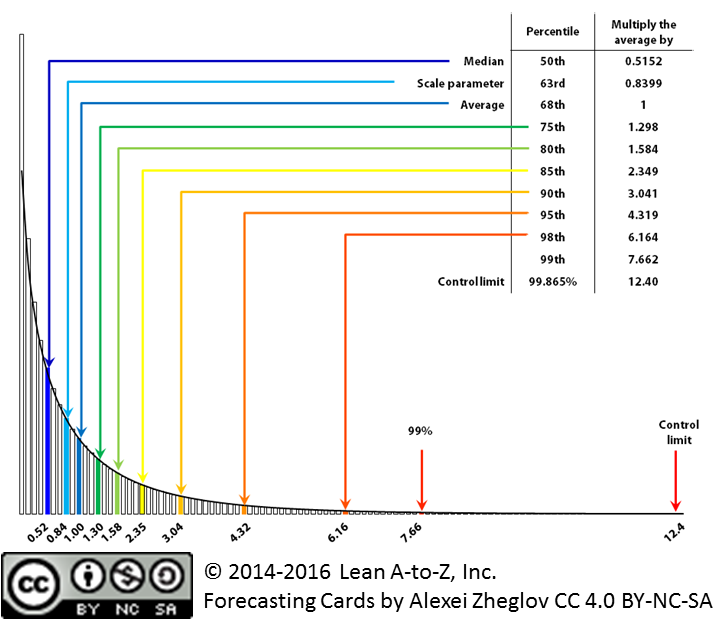
Когда значение параметра формы между 1 и 2, кривая вогнутая с левой стороны и до самого пика, с последующим переходом к выпуклости на склоне. Этот параметр формы наблюдают в средах продуктовой разработки. Я наблюдал значения параметра формы, близкие к 1 и 2 и все значение между ними. Стоит отметить, что значение между 1 и 1.5 наблюдаются чаще, чем значения между 1.5 и 2. Я выбрал k=1.5 и k=1.25, чтобы представить эту форму. Основные визуальные черты такого распределения:

• ассиметричный “горб”, резко растущий на левой стороне и плавно склоняющийся на правой
• мода (пик распределения) сдвинута влево (как я писал ранее, при k=1.25 и k=1.5, она попадает на 18 и 28 перцентили соответственно)
• медиана ненамного, но меньше среднего (87% от среднего при k=1.5)
• распространение общих причин вариации широкое, но уже, чем при k<1

В сфере разработки ПО, внедрение Agile-подходов может привести к смещение параметра формы влево. Этот эффект проявляется, потому что команды учатся поставлять код быстрее и в небольших партиях. Чтобы проиллюстрировать это, я включил в пост распределение с k=1.25.

Когда параметр формы больше 2, кривая выпуклая на левой стороне, переходящая к вогнутости до самого пика и снова переходит к выпуклости на склоне. Такую форму распределения часто наблюдают в поэтапных процессах. Я встречал этот тип кривой всего несколько раз. Самое большое значение параметра формы, которое я наблюдал: k=3.22. Я выбрал k=3 чтобы представить эту форму. Основная визуальная черта этого распределения — это намного более симметричный пик (но все еще асимметричный). При сравнении с k<2, распространение общих причин вариации уже относительно среднего значения. Тем не менее, процессы с таким типом распределения лид-таймов, зачастую имеют очень долгие средние лид-таймы.

Экспоненциальное распределение (k=1) фиксирует границу между двумя основными формами (k<1 и 1<k<2). Оно было очень хорошо изучено благодаря исследованиям теории массового обслуживания и цепей Маркова. Это распределение обладает уникальным качеством: функция отказов, которая выражает склонность завершить незавершенную работу, остается постоянной и независимой от времени. Если функция отказов со временем снижается, мы получаем распределения близкие к параметру формы k=1. Если он постепенно увеличивается, мы получим распределение близкое к показанным выше, с параметром формы 1<k<2.

Сходным образом, распределение Рэлея (k=2) фиксирует границу между формами k>2 и 1<2<k.

Сверка выборки с распределением Вейбулла

Первым шагом мы сужаем разброс значений параметра формы, наблюдая выпуклость-вогнутость на левой стороне и по центру.

Вторым шагом мы сопоставляем гистограмму выборки лид-таймов с примерами форм распределения из этого поста и проверяем, похожа ли она на один из примеров или находится между двумя. Соотношения перцентилей к среднему поможет в сопоставлении. Так мы получим параметр формы в довольно узком диапазоне (напр. от k=1.25 до k=1.5). Это менее точный, но достаточно достоверный метод для большинства практических применений. Он подойдет для обсуждения ожиданий уровня сервиса, контрольных лимитов или петель обратной связи.

Проверка вычислений

Кроме того, есть два простых количественных способа вычислить параметры формы и масштаба для распределения Вейбулла.

Довольно близкое значение к параметру масштаба находится у 63 перцентиля (еще раз спасибо Трою за подсказку). Действительно, значение функции накопительного распределения Вейбулла, где случайная переменная (лид-тайм) равняется параметру масштаба, независимо от параметра формы. Ее можно вычислить следующим образом:

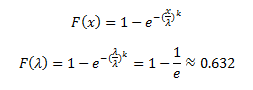
Значение функции квантилей (обратного накопительного распределения) в этой “волшебной точке” действительно равняется параметру масштаба, как показано ниже:

“Волшебная точка” обладает еще одним важным качеством, которое видим ниже:

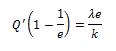
Если выборка лид-таймов достаточно плавная, чтобы допустить сопоставление склона функции квантилей на 63 перцентиле (напр. при использовании конечных разностей), то эту формулу можно использовать для вычисления параметра формы.

Итоги

• Распределение Вейбулла часто наблюдается в выборках лид-таймов из творческих сфер деятельности. Оценка параметров распределения (форма и масштаб) является желательной, чтобы использовать выборки в различных количественных моделях.
• Метод линейной регрессии всё ещё лучший вариант для нахождения параметров формы и масштаба.
• В ситуациях, когда специализированных инструментов нет под рукой, можно получить приближенные значения параметров формы и масштаба, сравнивая кривую с несколькими примерами. Важно различать три диапазона значений параметра формы (k<1, 1<k<2, k>2), наблюдая за выпуклостью и вогнутостью левой стороны и центра кривой распределения.
• Относительно низкая точность (две длины для параметров формы) достаточна для практического применения в быстрой оценке возможностей сервиса на основании выборки лид-таймов.
• Есть два математических трюка, основанных на уникальных особенностях распределения Вейбулла и 63 перцентиля. Их можно применить для приблизительного вычисления параметров распределения.

Оригинальная статья опубликована Алексеем Жегловым 8 сентября 2014
Перевод: Фролов Максим
Редактура: Артур Нек